唐磊的个人博客

关联规则-Apriori算法详解(附python版源码)

发表于 | 分类于 |

Apriori algorithm是关联规则里一项基本算法。是由Rakesh Agrawal和Ramakrishnan Srikant两位在1994年提出的布尔关联规则的频繁项集挖掘算法(详情：Fast Algorithms for Mining Association Rules)。算法的名字是因为算法基于先验知识(prior knowledge).根据前一次找到的频繁项来生成本次的频繁项。关联规则的目的在于在一个数据集中找出项之间的关系，也称之为购物蓝分析 (market basket analysis)。例如，购买佳能的顾客，有70%的可能也会买在一个月之类买HP打印机。这其中最有名的例子就是”尿布和啤酒“的故事了。

几个概念：

关联规则A->B的支持度support=P(AB)，指的是事件A和事件B同时发生的概率。置信度confidence=P(B|A)=P(AB)/P(A),指的是发生事件A的基础上发生事件B的概率。比如说在规则Computer => antivirus_software , 其中 support=2%, confidence=60%中，就表示的意思是所有的商品交易中有2%的顾客同时买了电脑和杀毒软件，并且购买电脑的顾客中有60%也购买了杀毒软件。

如果事件A中包含k个元素，那么称这个事件A为k**项集，并且事件A满足最小支持度阈值的事件称为频繁k项集**。

Apriori算法的基本思想：

过程分为两个步骤：第一步通过迭代，检索出事务数据库中的所有频繁项集，即支持度不低于用户设定的阈值的项集；第二步利用频繁项集构造出满足用户最小信任度的规则。具体做法就是：首先找出频繁1-项集，记为L1；然后利用L1来产生候选项集C2，对C2中的项进行判定挖掘出L2，即频繁2-项集；不断如此循环下去直到无法发现更多的频繁k-项集为止。每挖掘一层Lk就需要扫描整个数据库一遍。算法利用了一个性质：Apriori 性质：任一频繁项集的所有非空子集也必须是频繁的。意思就是说，生成一个k-itemset的候选项时，如果这个候选项有子集不在(k-1)-itemset(已经确定是frequent的)中时，那么这个候选项就不用拿去和支持度判断了，直接删除。具体而言：

1） 连接步

为找出Lk（所有的频繁k项集的集合），通过将Lk-1（所有的频繁k-1项集的集合）与自身连接产生候选k项集的集合。候选集合记作Ck。设l1和l2是Lk-1中的成员。记li[j]表示li中的第j项。假设Apriori算法对事务或项集中的项按字典次序排序，即对于（k-1）项集li，li[1]<li[2]<……….<li[k-1]。将Lk-1与自身连接，如果(l1[1]=l2[1])&&( l1[2]=l2[2])&&……..&& (l1[k-2]=l2[k-2])&&(l1[k-1]<l2[k-1])，那认为l1和l2是可连接。连接l1和l2 产生的结果是{l1[1],l1[2],……,l1[k-1],l2[k-1]}。

2） 剪枝步

CK是LK的超集，也就是说，CK的成员可能是也可能不是频繁的。通过扫描所有的事务（交易），确定CK中每个候选的计数，判断是否小于最小支持度计数，如果不是，则认为该候选是频繁的。为了压缩Ck,可以利用Apriori性质：任一频繁项集的所有非空子集也必须是频繁的，反之，如果某个候选的非空子集不是频繁的，那么该候选肯定不是频繁的，从而可以将其从CK中删除。

算法伪代码如下：

//算法：Apriori
//输入：D - 事务数据库；min_sup - 最小支持度计数阈值
//输出：L - D中的频繁项集
//方法：
     L1=find_frequent_1-itemsets(D); // 找出所有频繁1项集
     For(k=2;Lk-1!=null;k++){
        Ck=apriori_gen(Lk-1); // 产生候选，并剪枝
        For each 事务t in D{ // 扫描D进行候选计数
            Ct =subset(Ck,t); // 得到t的子集
            For each 候选c 属于 Ct
                         c.count++;
        }
        Lk={c属于Ck | c.count>=min_sup}
}
Return L=所有的频繁集；
 
Procedure apriori_gen(Lk-1:frequent(k-1)-itemsets)
      For each项集l1属于Lk-1
              For each项集 l2属于Lk-1
                       If((l1[1]=l2[1])&&( l1[2]=l2[2])&&……..
&& (l1[k-2]=l2[k-2])&&(l1[k-1]<l2[k-1])) then{
                   c=l1连接l2 //连接步：产生候选
                   if has_infrequent_subset(c,Lk-1) then
                       delete c; //剪枝步：删除非频繁候选
                   else add c to Ck;
                  }
          Return Ck;
 
     Procedure has_infrequent_sub(c:candidate k-itemset; Lk-1:frequent(k-1)-itemsets)
        For each(k-1)-subset s of c
            If s不属于Lk-1 then
               Return true;
        Return false;

举个例子,来源于书中(见参考文献1)的例子。

apriori算法

如图中所示,有9个事务，其算法流程如下：

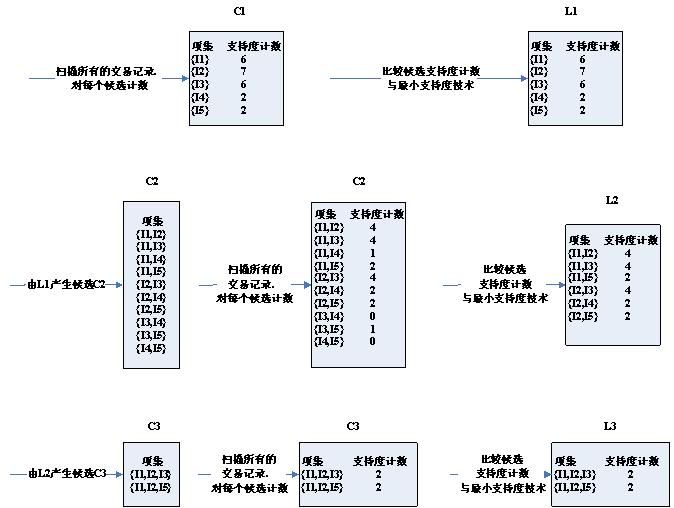
apriori算法,关联规则,数据挖掘

以上就有了频繁项集，然后根据得到的频繁项集和给定置信度算关联规则。置信度其实是一个条件概率。关联规则产生就是根据每个生成的频繁项集，产生其所有非空子集，然后根据子集和原来的事务库中循环比较。大于给定重复次数的就是满足条件的。例如针对频繁集{I1，I2，I5}。可以产生哪些关联规则？该频繁集的非空真子集（求子集的具体方法在前面python中a+=b和a=a+b的问题中已经阐述）有{I1，I2}，{I1，I5}，{I2，I5}，{I1 }，{I2}和{I5}，对应置信度如下：


I1&&I2->I5 confidence=2/4=50%


I1&&I5->I2 confidence=2/2=100%


I2&&I5->I1 confidence=2/2=100%


I1 ->I2&&I5 confidence=2/6=33%


I2 ->I1&&I5 confidence=2/7=29%


I5 ->I1&&I2 confidence=2/2=100%

如果min_conf=70%,则强规则有I1&&I5->I2，I2&&I5->I1，I5 ->I1&&I2。

 

具体而言：因为这几天在学python,所以就用python实现如下。里面有注释，刚开始用python，所以把一些问题也注释在里面了，代码可能不怎么清晰。仅供参考。

# coding=UTF-8
import copy
import re
import time
'''
Created on Mar 10, 2012

@author: tanglei|www.tanglei.name
'''
class Item:
    elements=[]
    supp=0.0
    def __init__(self,elements,supp=0.0):
        self.elements = elements
        self.supp = supp
    def __str__(self):
        returnstr = '[ '
        for e in self.elements:
            returnstr += e+','
        returnstr+=' ]'+' (support :%.3f)\t' %(self.supp)
        return returnstr
    def getSubset(self,k,size):
        subset=[]
        if k == 1:
            for i in range(size):
                subset.append([self.elements[i]])
            return subset 
        else:
            i = size - 1        
            while i >= k-1 :
                myset = self.getSubset(k-1,i)
                j = 0
                while j < len(myset):
                    #Attention a+=b  a=a+b  
                    myset[j] +=  [self.elements[i]]   #Why Elements change here?
                    j += 1
                subset += (myset)
                i -= 1
            return subset
        
    def lastDiff(self,items):
        length = len(self.elements)
        if length != len(items.elements):#length should be the same
            return False
        if self.elements == items:#if all the same,return false
            return False
        return self.elements[0:length-1] == items.elements[0:length-1]
    def setSupport(self,supp):
        self.supp = supp
        
    def join(self,items):
        temp = copy.copy(self.elements)
        temp.insert(len(self.elements), items.elements[len(items.elements) - 1])
        it = Item(temp,0.0)
        return it
#        self.elements.insert(len(self.elements), items.elements[len(items.elements) - 1])#Wrong,if so ,self.elements will change
#        it = Item(self.elements,0.0)
#        print(self.elements)
#        return it
    
#        the following is Wrong ,Because the Constructor Item(),First par is None
#        return copy.deepcopy(Item(\
#                                  self.elements.insert(\
#                                                       len(self.elements), items.elements[len(items.elements) - 1]\
#                                                       )\
#                                  ,0.0)\
#                             )
class C:
    '''candidate '''
    elements=[]
    k = 0 #order
    def __init__(self,elements,k):
        self.elements = elements
        self.k = k
        
    def isEmpty(self):
        if len(self.elements) == 0:
            return True
        return False
    #get the same order of itemsets whose support is at lease the threshold
    def getL(self,threshold):
        items=[]
        for item in self.elements:
            if item.supp >= threshold:
                items.append(copy.copy(item))
        if len(items) == 0:
            return L([],self.k)
        return L(copy.deepcopy(items),self.k)   
    
    def __str__(self):
        returnstr = str(self.k)+'-itemset:'+str(len(self.elements))+' \r\n{ '
        for e in self.elements:
            if True == isinstance(e,Item):
                returnstr += e.__str__()
        returnstr +=' }'
        return returnstr
    
class L:
    '''store all the  1-itemsets,2-itemsets,...k-itemsets'''
    items=[] #all the item in order K
    k=0  
    def __init__(self,items,k):
        self.items = items
        self.k = k
    def has_inFrequentItemsets(self,item):
#        return False
#        #先不优化
        subs = item.getSubset(self.k, len(item.elements))
        for each in subs:
            flag=False
            for i in self.items:
                if i.elements==each:
                    flag=True
                    break 
            if flag==False:
#                print("remove");print(item)
                return True  
        return False #there is at least one subset in the freq-items
        
    def aprioriGen(self):
        length=len(self.items)
        result=[]
        for i in range(length):
            for j in range(i+1,length):
                if self.items[i].lastDiff(self.items[j]):
                    item = self.items[i].join(self.items[j])
                    if False == self.has_inFrequentItemsets(item):#用Apriori性质：任一频繁项集的所有非空子集也必须是频繁的，反之，如果某个候选的非空子集不是频繁的，那么该候选肯定不是频繁的，从而可以将其从CK中删除。
                        result.append(item)
        if(len(result) == 0):
            return C([],self.k+1)
        return C(result,self.k+1)
    
    def __str__(self):
        returnstr="\r\n"+str(self.k) + '-itemsets :'+str(len(self.items))+"\r\n{"
        for item in self.items:
            returnstr += item.__str__()
        returnstr += '}'
        return returnstr
        
class LS:
    '''store from 1-itemset to k-itemset'''
    values={}#L1,L2,Lk
    def get(self,k):
        return self.values[k]
    def size(self):
        return len(self.values)
    def put(self,l,k):
        self.values[k]=l
    def isEmpty(self):
        return self.size()==0    
    def __str__(self):
        returnstr = '-----result--------\r\n'
        for l in self.values:
            returnstr += self.values[l].__str__()
        return returnstr
class Rule:
    confidence=.0
    str_rule=''
    def __init__(self,confidence,str_rule):
        self.confidence = confidence
        self.str_rule = str_rule
    def __str__(self):
        return 'Rule:' + self.str_rule + '  confidence:' + str(self.confidence)
      
class Apriori:
    def __init__(self,min_supp=0.07,datafile='apriori.test.data'):
        inputfile = open(datafile,"r")
        self.data=[]
        self.size=0
        self.min_supp = min_supp
        for line in inputfile.readlines():
            linearray = re.compile("[\d]+").findall(line)
            self.data.append(linearray)
        
        self.size=len(self.data)
        
    def  findFrequent1Itemsets(self):
        totalItemsets=[]
        for temp in self.data:
            totalItemsets.extend(temp)
        items = []#store the 1-itemset s
        
        while len(totalItemsets)>0:
            item=totalItemsets[0]
            count=0 
            j=0
            while j<len(totalItemsets):
                if (item == totalItemsets[j]) :
                    count += 1 
                    totalItemsets.remove(item) #remove the first occurence
                else:
                    j += 1
            t_supp = count/self.size
#            print(t_supp)
            
            if t_supp >= self.min_supp:
                items.append(Item([item],t_supp))
            
        temp = L(copy.deepcopy(items),1)
        return   temp
    def ralationRules(self,maxSequence,min_confidence):
        ruls=[]
        for each in maxSequence:
            for i in range(len(each.elements)-1):#real subsets 
                subsets = each.getSubset(i+1,len(each.elements))#get the subsets of the i+1 events
                for subset in subsets:
                    count=0
                    for tran_item in self.data:
                        flag = False #标记subset中的每个元素都在源中出现
                        for ele in subset:
                            if ele not in tran_item:
                                flag=True
                                break
                        if flag == False: #subset出现一次，计数
                            count += 1  
                    confidence = (each.supp*self.size)/count         
                    if  confidence >= min_confidence: #confidence/the number of the frequent pattern 
                        str_rule = str(set(subset)) + '-->' + str(set(each.elements)-set(subset))
                        rule =Rule(confidence,str_rule)           
                        ruls.append(rule)
        return ruls
          
    def do(self):      
        ls = LS()
        oneitemset = self.findFrequent1Itemsets()
        ls.put(oneitemset, 1)
        k = 2
        while False == ls.isEmpty():
            cand = ls.get(k - 1).aprioriGen()
            if cand.isEmpty():
                break
            for each in cand.elements:
                count = 0
                for each_src in self.data:
        #            count = each_src.count(each.elements)#only count the single element,can not be used to count if containing more than 2 elements
        #            need a function like Collection.containAll(Collection) in Java
                    if len(each_src)<len(each.elements):
                        pass
                    else:
        #不是必须连续 相等才满足条件，只要元素都在里面即可
        #                for i in range(len(each_src)):
        #                    if each.elements == each_src[i:len(each.elements)]:
        #                         break #no need continue ,We have supposed the elements be sequential
                        flag = True
                        for just_one_e in each.elements:
                                flag = just_one_e in each_src
                                if flag == False: #只要有一个不在，即退出
                                    break
                        if flag == True:   #当前候选事件都在的话，计数     
                            count += 1
                           
                supp = count/self.size
                each.setSupport(supp)
            ls.put(cand.getL(a.min_supp), k)
            k += 1
        return ls
  

starttime = time.time() 
a = Apriori(0.2,'apriori_blog.txt')
ls = a.do() 
print(ls) 
endtime =  time.time() 
print("It takes %d milliseconds to find the above  patterns" %((endtime-starttime) * 1000))    
print()
print(ls.get(ls.size()))
rules = a.ralationRules(ls.get(ls.size()).items,0.5)
for rule in rules:
    print(rule)

运行结果如下：

-----result--------

1-itemsets :5
{[ 1, ] (support :0.667)	[ 2, ] (support :0.778)	[ 5, ] (support :0.222)	[ 4, ] (support :0.222)	[ 3, ] (support :0.667)	}
2-itemsets :6
{[ 1,2, ] (support :0.444)	[ 1,5, ] (support :0.222)	[ 1,3, ] (support :0.444)	[ 2,5, ] (support :0.222)	[ 2,4, ] (support :0.222)	[ 2,3, ] (support :0.444)	}
3-itemsets :2
{[ 1,2,5, ] (support :0.222)	[ 1,2,3, ] (support :0.222)	}
It takes 0 milliseconds to find the above  patterns


3-itemsets :2
{[ 1,2,5, ] (support :0.222)	[ 1,2,3, ] (support :0.222)	}
Rule:{'5'}-->{'1', '2'}  confidence:1.0
Rule:{'1', '5'}-->{'2'}  confidence:1.0
Rule:{'2', '5'}-->{'1'}  confidence:1.0
Rule:{'1', '2'}-->{'5'}  confidence:0.5
Rule:{'1', '3'}-->{'2'}  confidence:0.5
Rule:{'3', '2'}-->{'1'}  confidence:0.5
Rule:{'1', '2'}-->{'3'}  confidence:0.5

有网友指出，本页代码在其python环境运行结果不正确，因其环境用的是python2.x，而本人用的环境是python3.x，在python3.x中，两个整数相除是得到小数的，而python2.x里是整数，因此导致支持度计算不正确，只需要改正本页代码中的196行和256行将分子转换成浮点即可（例如分别改为t_supp = count*1.0/self.size，supp = count*1.0/self.size）。本人初学python，一些细节不清楚，望理解。感谢网友指出。

参考文献：

Jiawei Han and Micheline Kamber.Data Mining: Concepts and Techniques[M]. San Francisco: Morgan Kaufmann Publishers.2006：234-240

http://blog.sina.com.cn/s/blog_4882f26d0100spl1.html

tanglei wechat
欢迎扫码加入互联网大厂内推群 & 技术交流群，一起学习、共同进步